PlayStation: The SPU, Part 2 - Volume

Where the last post focused on the PlayStation SPU’s audio format and how to implement ADPCM decoding, this post will focus on volume and envelopes. The SPU supports a number of different volume multipliers: some as constant volumes, and some as volumes that automatically adjust themselves over time using what are called envelope generators.

ADSR

In the context of audio in general, an envelope describes how a sound changes over time. In the context of most gaming console sound chips, the envelope generator is responsible for automatically adjusting volume over time.

The most primitive console sound chips (e.g. the Sega Master System PSG) don’t have envelopes at all. Channels can only play at a fixed constant volume.

Slightly more advanced sound chips such as the Game Boy APU and the NES APU have linear envelopes that can increase or decrease volume at a configurable linear rate, all the way up to max volume or all the way down to muted. This is better than having no envelopes at all but linear envelopes are pretty limited, especially in these older sound chips where the envelope volume is only a 4-bit value.

In the next generation of consoles, both the Genesis YM2612 and the SNES APU support what are called ADSR envelopes, which allow for much more advanced automatic volume adjustment. The PS1 SPU also supports ADSR envelopes.

ADSR stands for “Attack, Decay, Sustain, Release”, which are the four phases that an ADSR envelope progresses through. The basic idea is to mimic the volume progression that occurs when you press a real-life piano key.

Here is the obligatory diagram that appears in any description of ADSR:

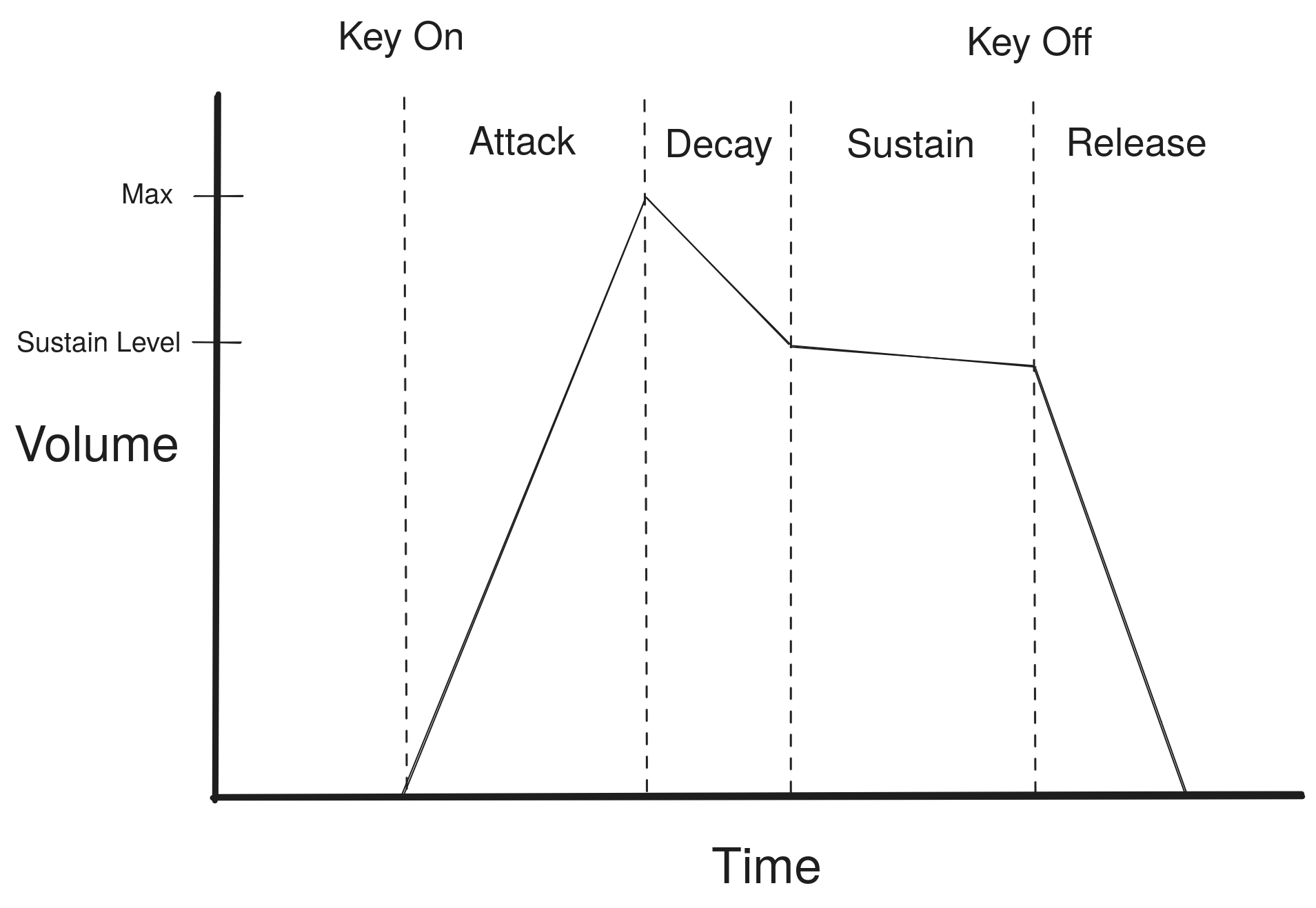
When the key is first pressed (“key on”), the volume increases fairly rapidly from complete silence to the maximum possible volume. This is called the Attack phase.

After the volume reaches max during the Attack phase, it begins to rapidly decrease from the volume peak. This is called the Decay phase.

At a certain point during the Decay phase, the volume stops decreasing rapidly, and it instead begins to decrease slowly for as long as the key is held down. This is called the Sustain phase, and the volume at which the Decay-to-Sustain switch occurs is called the sustain level. (Note that real implementations will sometimes hold the volume constant instead of gradually decreasing it, and the PS1 SPU even supports an option to gradually increase volume during Sustain phase.)

When the key is released (“key off”), the volume begins to decrease very rapidly all the way down to complete silence, regardless of what phase the envelope was in before. This is called the Release phase.

A sound chip that supports ADSR envelopes will perform these phase and volume transitions automatically. Software can configure some settings (e.g. volume change rate) that affect how the different phases will behave, and then it can direct the envelope generator by sending key on and key off events.

Volume Multipliers

In the PS1 SPU, all volumes are signed 16-bit integers that represent a value N/0x8000. This means that volume multipliers are effectively always decreases, since the maximum possible magnitude of a signed 16-bit integer is 0x8000 (32768 in decimal). All volume multipliers can be applied as such:

1
2
3
4

fn apply_volume(sample: i16, volume: i16) -> i16 {
    // Do multiplication in 32 bits to avoid possible overflow
    ((i32::from(sample) * i32::from(volume)) >> 15) as i16
}

N >> 15 is technically not equivalent to N / 0x8000 when N is a negative number less than 0x8000, but I personally think it’s pretty unlikely that the hardware divides rather than bit shifts simply because division is more expensive. It’s also not a huge difference in practice because -1 vs. 0 is tiny on a scale from -32768 to +32767.

The SPU has a number of different volume multipliers:

• Per-voice overall volume (from fully configurable ADSR envelopes)
• Per-voice left and right volumes (either constant or from limited sweep envelopes)
• Main left and right volumes (either constant or from limited sweep envelopes)

So, to get the samples from a voice, you could do something like this (pretending for now that the voice L/R volumes are always constant):

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19

struct Voice {
    envelope: AdsrEnvelope,
    volume_l: i16,
    volume_r: i16,
    ...
}

impl Voice {
    fn apply_voice_volume(&self, adpcm_sample: i16) -> (i16, i16) {
        // Apply ADSR envelope first
        let envelope_sample = apply_volume(adpcm_sample, self.envelope.level);

        // Apply L/R volumes second
        let output_l = apply_volume(envelope_sample, self.volume_l);
        let output_r = apply_volume(envelope_sample, self.volume_r);

        (output_l, output_r)
    }
}

Note that we’re now generating two output samples for each voice: one for the left audio channel and one for the right audio channel. They’re both derived from the same interpolated ADPCM sample, but possibly using different volume multipliers.

The main volumes are applied after mixing the 24 voices together:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

struct Spu {
    voices: [Voice; 24],
    main_volume_l: i16,
    main_volume_r: i16,
    ...
}

impl Spu {
    fn sample(&self) -> (i16, i16) {
        // Add all the voice samples together
        let mut mixed_l = 0_i32;
        let mut mixed_r = 0_i32;
        for voice in &self.voices {
            let (voice_sample_l, voice_sample_r) = voice.current_sample;
            mixed_l += i32::from(voice_sample_l);
            mixed_r += i32::from(voice_sample_r);
        }

        // Clamp the sums to signed 16-bit
        let clamped_l = mixed_l.clamp(-0x8000, 0x7FFF) as i16;
        let clamped_r = mixed_r.clamp(-0x8000, 0x7FFF) as i16;

        // Apply main volume after mixing
        let output_l = apply_volume(clamped_l, self.main_volume_l);
        let output_r = apply_volume(clamped_r, self.main_volume_r);

        (output_l, output_r)
    }
}

I’m not completely confident that this example mixing code is exactly correct in terms of when clamping is applied (it could theoretically be applied after adding each voice sample), but at worst this might produce a “better” result than actual hardware in overflow scenarios.

So, that’s how to apply the volume multipliers. How are they generated?

Envelope Updates

Each voice has a fully configurable ADSR envelope that is configured using two registers:

• $1F801C08 + N*$10: Attack settings, decay settings, sustain level
• $1F801C0A + N*$10: Sustain settings, release settings

Each of the four phases has the same parameters:

• Direction: Increasing or decreasing
• Change Rate Mode: Linear or exponential
• Change Shift: 5-bit integer that determines the coarse update speed
• Change Step: 2-bit integer that determines the fine update speed

However, not every parameter is configurable in every phase:

To state it very explicitly, the envelope functions the same way in every phase. The only thing that differs between phases is how the envelope determines what values to use for direction/rate/shift/step.

Sustain is the most configurable phase and Decay is the least configurable.

“Step” is a 2-bit value that is interpreted as (7 - N) when increasing and -(8 - N) when decreasing. For Decay and Release phases the raw step is fixed to 0, which is interpreted as -8.

“Shift” is essentially the core change rate as a power of two, with higher values indicating a slower change rate. A shift value of 11 is the baseline, where the envelope updates every SPU clock cycle and the step parameter is used as-is. Shift values higher than 11 cause the envelope to update less frequently. Shift values lower than 11 don’t affect the envelope update rate (it still updates every SPU cycle), but they make the updates larger by left shifting the step parameter.

Exponential decrease works by decreasing the effective step value as the envelope volume approaches 0. Exponential increase is faked and simply slows down the update rate when the envelope volume crosses a threshold of 0x6000.

psx-spx has pseudocode for the envelope update here, but using that implementation as-is will not work with some games. The main problem with this pseudocode implementation is that some games will change envelope settings of keyed-on envelopes in the middle of Attack/Decay/Sustain phase, and that needs to immediately affect the number of “wait cycles” instead of waiting until the wait cycle counter reaches 0. Final Fantasy VII is one example of a game that depends on this or else some sound effects will play incorrectly.

I don’t really know what actual hardware does here, but I handle the wait cycles using per-envelope downcounters. The counter is initialized to the maximum possible number of cycles between envelope updates, and each envelope clock decrements the counter by a value determined from the current parameters. When the counter reaches 0, the envelope updates its volume and the counter resets to max.

The maximum number of cycles between updates is 1 << (33 - 11) which is used when the shift is 31, the envelope is set to exponential increase mode, and the current volume is greater than 0x6000.

First, let’s define some enums:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11

#[derive(Debug, Clone, Copy, PartialEq, Eq)]
enum Direction {
    Increasing,
    Decreasing,
}

#[derive(Debug, Clone, Copy, PartialEq, Eq)]
enum ChangeRate {
    Linear,
    Exponential,
}

We can handle the wait cycles like this:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27

const ENVELOPE_COUNTER_MAX: u32 = 1 << (33 - 11);

struct AdsrEnvelope {
    level: i16,
    counter: u32,
    ...
}

impl AdsrEnvelope {
    fn clock(&mut self, direction: Direction, rate: ChangeRate, shift: u8) {
        // For a shift value of N, the envelope should update every 1 << (N - 11) cycles.
        // Accomplish this by using a counter decrement of MAX >> (N - 11)
        let mut counter_decrement = ENVELOPE_COUNTER_MAX >> shift.saturating_sub(11);
        
        // Quadruple the update interval if in exponential increase mode and volume is above the threshold
        if direction == Direction::Increasing && rate == ChangeRate::Exponential && self.level > 0x6000 {
            counter_decrement >>= 2;
        }

        self.counter = self.counter.saturating_sub(counter_decrement);
        if self.counter == 0 {
            self.counter = ENVELOPE_COUNTER_MAX;

            todo!("update envelope")
        }
    }
}

The envelope update calculation is straightforward, since it’s pretty much just the psx-spx pseudocode:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

impl AdsrEnvelope {
    fn update(&mut self, direction: Direction, rate: ChangeRate, shift: u8, step: u8) {
        // Step is interpreted as (7 - N) if increasing and -(8 - N) if decreasing
        // -(8 - N) is just the 1's complement of (7 - N)
        let mut step = i32::from(7 - step);
        if direction == Direction::Decreasing {
            step = !step;
        }

        // If shift is less than 11, step is left shifted
        step <<= 11_u8.saturating_sub(shift);

        // In exponential decrease mode, use current volume as a multiplier
        // This has the effect of slowing updates at lower volumes
        let current_level: i32 = self.level.into();
        if direction == Direction::Decreasing && rate == ChangeRate::Exponential {
            step = (step * current_level) >> 15;
        }

        // Apply step and clamp to an unsigned 15-bit integer
        self.level = (current_level + step).clamp(0, 0x7FFF) as i16;
    }
}

That’s about it for the updates, but the envelope needs to know the current phase in order to determine which set of parameters to use.

Envelope Phases

ADSR envelopes are in the Release phase by default.

Keying on a voice immediately sets the volume to 0 (if it isn’t already) and sets the phase to Attack.

The envelope automatically transitions from Attack to Decay when it reaches the max volume level of 0x7FFF.

The envelope automatically transitions from Decay to Sustain when the volume reaches (or passes) the sustain level, and it remains in Sustain phase until the voice is keyed off.

Keying off a voice immediately sets the phase to Release (and has no immediate effect on volume). It does not matter what phase the envelope was in before.

The envelope phase transitions are simpler to handle than the updates. You can do something like this:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

#[derive(Debug, Clone, Copy, PartialEq, Eq)]
enum AdsrPhase {
    Attack,
    Decay,
    Sustain,
    Release,
}

struct AdsrEnvelope {
    phase: AdsrPhase,
    level: i16,
    sustain_level: u16,
    ...
}

impl AdsrEnvelope {
    fn key_on(&mut self) {
        self.level = 0;
        self.phase = AdsrPhase::Attack;
    }

    fn key_off(&mut self) {
        self.phase = AdsrPhase::Release;
    }

    fn check_for_phase_transition(&mut self) {
        if self.phase == AdsrPhase::Attack && self.level == 0x7FFF {
            self.phase = AdsrPhase::Decay;
        }

        // Note that the envelope should go straight from Attack to Sustain if the sustain level is
        // set to the highest possible value
        if self.phase == AdsrPhase::Decay && (self.level as u16) <= self.sustain_level {
            self.phase = AdsrPhase::Sustain;
        }
    }
}

Then the clock() method needs to check for a phase transition before computing the counter decrement, and it should select the appropriate direction/rate/shift/step values based on the current phase.

That’s just about it for the ADSR envelopes! Each voice has one of these and they all operate independently of each other.

Sweep Envelopes

The L/R volumes can be set to a fixed value or they can use envelopes, which documentation refers to as sweep envelopes. This applies to both the individual voice L/R volumes and the main L/R volumes. These sweep envelopes are more limited than the ADSR envelopes but they work pretty similarly.

The stereo volumes are configured using these registers:

• $1F801C00 + N*$10: Voice N left volume
• $1F801C02 + N*$10: Voice N right volume
• $1F801DB8: Main left volume
• $1F801DBA: Main right volume

Bit 15 determines whether the volume is constant or using an envelope. If bit 15 is clear then the volume is constant, and the lower 15 bits determine the volume value. The 15 bits are interpreted as a signed 15-bit integer equal to half the desired volume, so the actual volume value is (value << 1) as i16.

If bit 15 is set, then the volume value is left unchanged and an envelope is configured using envelope parameters specified in the lower 15 bits. The envelope uses the same direction/rate/shift/step parameters as the ADSR envelopes, but these sweep envelopes don’t have ADSR phases, so the configured parameters are used indefinitely.

The clocks and updates work the same as for the ADSR envelopes except there are no phase transitions, and the envelope volume is a signed 16-bit integer rather than an unsigned 15-bit integer. Negative volume values work the same as positive values except they invert the sample’s sign during the volume multiplication.

The sweep envelopes have an additional parameter that psx-spx calls “sweep phase” which can be set to positive or negative. This seems to interact with the fact that sweep envelope volumes can be negative. Documentation is unclear on what exactly it does, but it seems like setting it to negative inverts increasing/decreasing so that the volume “increases” from 0 to -0x7FFF and “decreases” from -0x7FFF to 0. The sweep phase bit apparently does not work properly in exponential decrease mode, though it’s unclear to me exactly how.

Testing It

With all of the above volume/envelope functionality implemented, the BIOS startup sounds much better!

It does still sound slightly wrong compared to the real thing though. That’s because it’s missing reverb.

To Be Continued

I plan to do one more post on the SPU covering the remaining major features: reverb, pitch modulation, and noise generation.