Emulating the YM2612: Part 2 - Phase

This is the second in a series of posts on emulating the main Sega Genesis sound chip, the YM2612.

This post will describe the FM synthesis channels’ phase generators.

Phase Generation

Each of the YM2612’s 24 operators contains a phase generator and an ADSR envelope generator. The phase generator determines the current phase within the sine wave, and the envelope generator determines the amount of attenuation to apply to the sine wave’s amplitude.

Each operator’s phase generator is clocked once every 24 YM2612 internal cycles, or equivalently once per 53267 Hz output sample. In actual hardware, the chip’s 24 operators are clocked roughly sequentially during the 24 cycles between output samples (with some pipelining), but emulators typically clock the 24 operators all at once every 24 cycles. It doesn’t make an audible difference given how software interacts with the chip.

The phase generator ultimately outputs a 10-bit integer that represents a number ranging from 0 to 2π, and this is used as input to the sine function.

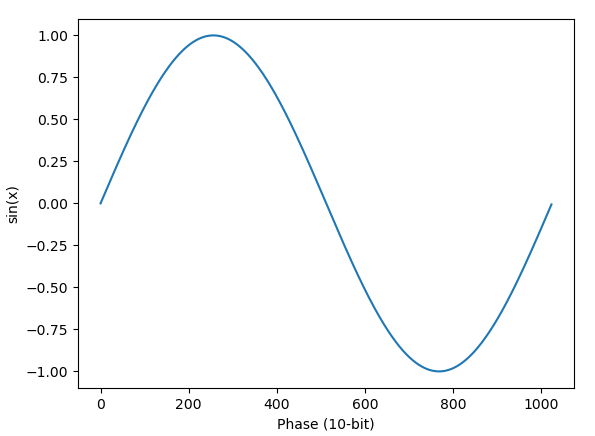
Phase Sine

Inputs

Each phase generator has 5 inputs:

F-number (11-bit), i.e. base frequency
Block (3-bit), i.e. octave
Detune (3-bit)
Multiple (4-bit)
LFO FM sensitivity (3-bit), i.e. vibrato level

Detune and multiple are configured per-operator while F-number, block, and FM sensitivity are configured per-channel. These are configured using the following YM2612 registers:

$30-$3F: Multiple (Bits 0-3) and detune (Bits 4-6)
$A0-$A2: F-number, lowest 8 bits
$A4-$A6: F-number, highest 3 bits (Bits 0-2) and block (Bits 3-5)
$B4-$B6: LFO FM sensitivity (Bits 0-2), plus other values not used by phase generator

One fairly important thing to note is that writes to $A4-$A6 (F-num high + block) do not actually take effect until after writing to the paired F-num low register at $A0-$A2, which applies the most recent writes to both frequency registers. Some games will have slightly broken audio if $A4-$A6 writes take effect immediately, such as Valis. It likes to key on operators with a frequency of 0 and then later change the frequency to a real value. This only works correctly if the two frequency register writes are applied simultaneously after the $A0-$A2 write.

Where most of the channels use the same F-number and block for all 4 operators, channel 3 is special: it supports a mode where each of the 4 operators can have its own F-number and block. This mode is enabled by writing to register $27 with bit 6 or 7 set (value & 0xC0 != 0). When this special mode is enabled, $A2 and $A6 only control operator 4’s F-number and block, and channel 3’s other 3 operators are configured using the following registers:

Operator 1: $A9 (low) and $AD (high + block)
Operator 2: $AA (low) and $AE (high + block)
Operator 3: $A8 (low) and $AC (high + block)

Yes, the mapping from register address to operator number is a bit strange, but that’s what’s in the YM2608 manual and it seems to be accurate. Similar to the per-channel registers, writes to the F-num high + block registers are not applied until after writing to the paired F-num low register.

Note that $27 is also the timer control register - the lower 6 bits are used to control the two hardware timers. Also, writing to $27 with bit 7 set and bit 6 clear (value & 0xC0 == 0x80) enables a mode called CSM in addition to enabling channel 3’s per-operator frequency mode. CSM was meant for speech synthesis, but as far as I know no games used it, and some emulators don’t emulate it at all.

Base Frequency

Let’s start by looking only at the two frequency-related inputs: F-number and block.

These two values together determine the sine wave base frequency. The YM2608 manual contains a formula that reveals the relationship between these values and wave frequency: Frequency Formula

This can be rewritten as:

fnote = (Fnum ⋅ 2^B-1 / 2²⁰) ⋅ (M / 144)

A change of 1 in Fnum * 2^B-1 corresponds to a frequency change of about 0.051 Hz with a 7.67 MHz master clock:

1
2


>>> 7.67e6 / 144 / 2**20
0.05079640282524957

The maximum possible base frequency is about 6655 Hz:

1
2


>>> ((1 << 11) - 1) * 2**(7-1) * 7.67e6 / 144 / 2**20
6654.735141330295

M/144 is the rate at which the phase generator is clocked (M / 6 / 24), and therefore the rest of the formula represents the phase increment at each phase generator clock, on a scale where 1 is equal to a full 0-to-2π wave oscillation:

increment = Fnum ⋅ 2^B-1 / 2²⁰

The chip implements this internally using a 20-bit phase counter, hence the 2²⁰ divisor. At each clock it increments the counter by the F-number, but bit shifted based on the block value. If block is 0 then F-number is right shifted by 1, otherwise F-number is left shifted by (B-1). This is equivalent to a left shift of B followed by a right shift of 1, which doesn’t require special casing block 0.

The phase generator’s 10-bit output is simply the highest 10 bits of this 20-bit phase counter.

Example implementation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21


struct PhaseGenerator {
    counter: u32, // 20-bit
    f_number: u32, // 11-bit
    block: u8, // 3-bit
}

impl PhaseGenerator {
    // 7.67 MHz / 144 clock
    fn clock(&mut self) {
        // Shift F-number based on block; this produces a 17-bit value
        let increment = (self.f_number << self.block) >> 1;

        // Increment counter, mask to 20 bits
        self.counter = (self.counter + increment) & ((1 << 20) - 1);
    }

    fn output(&self) -> u32 {
        // Phase generator output is highest 10 bits of 20-bit phase counter
        self.counter >> 10
    }
}

Detune

Detune is a feature that very slightly increases or decreases an operator’s base frequency relative to the channel’s base frequency. Applying different levels of detune to multiple carriers with the same base frequency produces a richer sound than playing two notes exactly in tune. Using detune with modulators makes it possible to produce very complex waveforms.

In the YM2612, detune is a 3-bit value. The highest bit indicates whether to increase (0) or decrease (1) the frequency, and the lowest two bits indicate the magnitude of the frequency change. If the lowest two bits are both 0, detune is disabled, i.e. the frequency change is always 0.

One thing that makes detune slightly tricky is that the magnitude of the frequency change varies based on F-number and block. When the base frequency is higher, the detune frequency change is larger. This is necessary to ensure that the detune effect is audible at higher frequencies.

The YM2612 implements detune using a lookup table based on a value that the YM2608 manual refers to as “key code”. The key code encapsulates the combined F-number and block into a 5-bit value that the chip uses to index into 32-entry lookup tables.

Key code is computed like so:

Bits 4-2 = Block
Bit 1 = F11
Bit 0 = (F11 & (F10 | F9 | F8)) | (!F11 & F10 & F9 & F8)

F11 through F8 are the four highest bits of F-number, F11 being the highest bit.

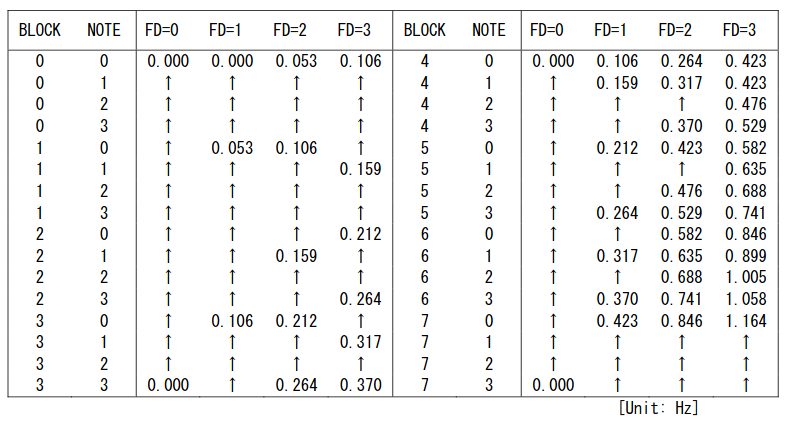
The YM2608 manual includes the entire 32x4 lookup table, described using frequency values in Hz. “NOTE” is the lowest two bits of the key code and “FD” is the lowest two bits of detune: Detune Table

These frequency values are based on an 8 MHz master clock, as are all the other frequency values in the YM2608 manual. Knowing that, it’s pretty easy to confirm that 0.053 Hz in this table is equal to a change of 1 in the phase increment value:

1
2


>>> 0.053 * 144 * 2**20 / 8e6
1.0003415039999999

The actual lookup table is a table of phase increment deltas, not frequency values. Doing the conversion is just busy work, so here’s the converted table:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10


const DETUNE_TABLE: &[[u8; 4]; 32] = &[
    [0,  0,  1,  2],  [0,  0,  1,  2],  [0,  0,  1,  2],  [0,  0,  1,  2],  // Block 0
    [0,  1,  2,  2],  [0,  1,  2,  3],  [0,  1,  2,  3],  [0,  1,  2,  3],  // Block 1
    [0,  1,  2,  4],  [0,  1,  3,  4],  [0,  1,  3,  4],  [0,  1,  3,  5],  // Block 2
    [0,  2,  4,  5],  [0,  2,  4,  6],  [0,  2,  4,  6],  [0,  2,  5,  7],  // Block 3
    [0,  2,  5,  8],  [0,  3,  6,  8],  [0,  3,  6,  9],  [0,  3,  7, 10],  // Block 4
    [0,  4,  8, 11],  [0,  4,  8, 12],  [0,  4,  9, 13],  [0,  5, 10, 14],  // Block 5
    [0,  5, 11, 16],  [0,  6, 12, 17],  [0,  6, 13, 19],  [0,  7, 14, 20],  // Block 6
    [0,  8, 16, 22],  [0,  8, 16, 22],  [0,  8, 16, 22],  [0,  8, 16, 22],  // Block 7
];

You could instead store it as a &[[u8; 3]; 32] if you wanted since the delta is always 0 if the lowest two bits of detune are 0.

The maximum possible phase increment delta is 22, which corresponds to a frequency change of roughly 1.118 Hz with a 7.67 MHz master clock:

1
2


>>> 22 * 7.67e6 / 144 / 2**20
1.1175208621554904

Once the detune table and key code calculation are in place, applying detune is just a table lookup followed by an addition or subtraction.

There is one quirk related to detune: The post-detune phase increment is still a 17-bit value, same as the block-shifted F-number. This is important because when frequency is very low, it’s possible for subtractive detune to overflow from 0 to 0x1FFFF. Some games depend on handling detune overflow correctly, particularly games that use the GEMS sound driver’s builtin instruments - some of them depend on subtractive detune overflowing to 0x1FFFF instead of 0xFFFFF.

Additive detune cannot normally overflow because the highest possible pre-detune increment is 0x1FFC0, which becomes 0x1FFD6 after adding the highest possible detune value. However overflow is possible when additive detune is combined with vibrato / LFO FM, so it’s always necessary to mask the post-detune increment to 17 bits.

Adding to the example implementation:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37


// New function to compute key code
fn compute_key_code(f_number: u32, block: u8) -> u8 {
    // Definition omitted
}

struct PhaseGenerator {
    counter: u32,
    f_number: u32,
    block: u8,
    detune: u8, // New field: 3-bit
}

impl PhaseGenerator {
    // 7.67 MHz / 144 clock
    fn clock(&mut self) {
        // Apply block; produces 17-bit result
        let mut increment = (self.f_number << self.block) >> 1;

        // New code: Apply detune
        let key_code = compute_key_code(self.f_number, self.block) as usize;
        let detune_idx = (self.detune & 3) as usize;
        let detune_magnitude: u32 = DETUNE_TABLE[key_code][detune_idx].into();
        increment = if self.detune & (1 << 2) != 0 {
            // Subtractive detune; decrease frequency
            // This can overflow!
            increment.wrapping_sub(detune_magnitude)
        } else {
            // Additive detune; increase frequency
            increment.wrapping_add(detune_magnitude)
        };

        // Mask post-detune increment to 17 bits (required to handle detune overflow correctly)
        increment &= (1 << 17) - 1; 

        self.counter = (self.counter + increment) & ((1 << 20) - 1);
    }
}

Multiple

Multiple functions as a per-operator frequency multiplier. All 4 operators within a channel must use the same base frequency (barring channel 3’s special mode), but this feature allows each operator to use a different multiple of the base frequency.

Effective multiplier values range from 0.5x to 15x the base frequency. A 4-bit multiple value of 0 functions as a multiplier of 0.5, i.e. a right shift by 1, while any other value M functions as a multiplier of M.

Multiple is applied last, after block and detune.

The result of applying multiple is a 20-bit value, same as the phase counter. The multiplication can produce a 21-bit result; in this case the highest bit is simply ignored, i.e. the phase increment wraps from 0xFFFFF to 0.

This is straightforward to add to the above example code:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28


struct PhaseGenerator {
    counter: u32,
    f_number: u32,
    block: u8,
    detune: u8,
    multiple: u32, // New field: 4-bit
}

impl PhaseGenerator {
    // 7.67 MHz / 144 clock
    fn clock(&mut self) {
        // Block; produces 17-bit value
        let mut increment = (self.f_number << self.block) >> 1;

        // Detune; produces 17-bit value
        increment = self.apply_detune(increment) & ((1 << 17) - 1);

        // New code: Apply multiple
        // Produces 20-bit value
        increment = match self.multiple {
            0 => increment >> 1,
            m => increment * m,
        };
        // No need to explicitly mask to 20-bit here because the phase counter is masked to 20-bit after adding

        self.counter = (self.counter + increment) & ((1 << 20) - 1);
    }
}

If you wanted to avoid the branch checking whether multiple is 0, you could create a 16-entry lookup table where each entry contains double the multiplier value:

1

[2*n if n >= 1 else 1 for n in range(16)]

Then you can unconditionally multiply and right shift by 1 afterwards:

1

increment = (increment * MULTIPLE_TABLE[self.multiple as usize]) >> 1;

I do not know if this is actually faster on modern CPUs, or if the difference is even non-negligible. It almost certainly depends on how frequently multiple 0 is used.

That’s pretty much it for the core phase generator functionality, aside from vibrato / LFO FM which I will save for a later post discussing the LFO in more detail. At a very high level, vibrato automatically varies an operator’s F-number over time when enabled. The globally configured LFO frequency determines how rapidly the frequency varies, and the channel’s LFO FM sensitivity determines the magnitude of the frequency variation.

Keying On

One last thing to mention with the phase generators is that keying on an operator resets the phase generator’s internal 20-bit counter to 0. Most of the effects of keying on/off are related to the envelope generators, but keying on does also reset the phase counter.

Operators are keyed on and off by writing to register $28. The lowest 3 bits of the value determine the target channel:

000 = Channel 1
001 = Channel 2
010 = Channel 3
100 = Channel 4
101 = Channel 5
110 = Channel 6
011 / 111 = Invalid

Then, the highest 4 bits control the key on or off state of each operator in that channel:

Bit 4 = Operator 1 (1=key on, 0=key off)
Bit 5 = Operator 2
Bit 6 = Operator 3
Bit 7 = Operator 4

Keying on an operator that is already keyed on has no effect. Keying on a keyed-off operator resets the phase counter to 0.

Keying off has no effect on the phase generator, only on the envelope generator.

Operator Output V0

It would be nice to wire this up to audio output to try and validate that it’s even remotely correct. Let’s try it!

To be clear, you don’t have to do any of this because it is 100% throwaway code, but I think it’s nice to get some audio output earlier rather than later.

Phase modulation is not going to work even remotely properly without ADSR envelopes implemented, so let’s not do that. In fact, for now, let’s ignore the algorithm entirely and have each channel use operator 4’s output as the channel output. Operator 4 is a carrier in all 8 algorithms.

We can simulate “volume” using the key on/off state of each operator. If the operator is keyed on, play it at a constant volume. If it’s keyed off, mute it.

Actual hardware converts the 10-bit phase value to a log2-sine value using lookup tables. For now, let’s just compute the sine using floating-point math.

And so:

 1
 2
 3
 4
 5
 6
 7
 8
 9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48


struct FmOperator {
    phase: PhaseGenerator,
    key_on: bool,
}

struct FmChannel {
    operators: [FmOperator; 4],
}

impl FmChannel {
    // 7.67 MHz / 144 clock
    fn clock(&mut self) -> f64 {
        use std::f64::consts::PI;

        // Ignore algorithm and always use operator 4's output
        let carrier = &mut self.operators[3];
        if !carrier.key_on {
            return 0.0;
        }

        carrier.phase.clock();
        let phase = carrier.phase.output();

        // Phase is a 10-bit integer; convert to [0, 2*PI)
        let phase = f64::from(phase) / f64::from(1 << 10) * 2.0 * PI;

        // Compute sine and use as channel output
        phase.sin()
    }
}

struct Ym2612 {
    channels: [FmChannel; 6],
}

impl Ym2612 {
    // 7.67 MHz / 144 clock
    fn sample_clock(&mut self) -> f64 {
        let mut sum = 0.0;
        for channel in &mut self.channels {
            // Multiply by an arbitrary fraction to prevent every channel playing at max volume
            sum += 0.3 * channel.clock();
        }

        // Divide by 6 because there are 6 channels
        sum / 6.0
    }
}

The DAC channel should replace channel 6’s output if it is active, but other than that, this should produce…something?

Let’s see:

Sonic the Hedgehog 2 - Emerald Hill Zone

Well…that really doesn’t sound like the YM2612 at all since it’s just plain sine waves, but the melody is very recognizable! Progress!

To Be Continued

The next post will cover one of the trickier parts of the YM2612 to emulate correctly: the envelope generators.

Part 3 - Envelopes

Emulating the YM2612: Part 2 - Phase

See Also: